MATEMÁTICAS PARA NIÑOS
CUADRADOS MÁGICOS
CONCEPTO
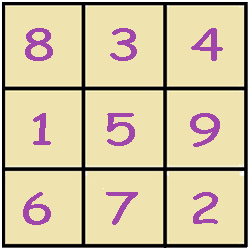
Los cuadrados mágicos son distribuciones de números en celdas que se disponen formando un cuadrado, de forma que la suma de cualquiera de las filas, de cualquiera de las columnas y de las dos diagonales principales da siempre el mismo resultado. Al número resultante se le denomina «constante mágica».
Por ejemplo, en el siguiente cuadrado mágico se han dispuesto los números del 1 al 9. Puede comprobarse que su «constante mágica» es 15, es decir, la suma de sus filas, columnas y diagonales es 15.
TIPOS DE CUADRADOS MÁGICOS
Si el cuadrado mágico tiene tres filas y tres columnas, es decir nueve casillas y por lo tanto nueve números, se denomina cuadrado mágico de orden tres.
Si el cuadrado mágico tiene cuatro filas y cuatro columnas, es decir dieciséis casillas y dieciséis números, se denomina cuadrado mágico de orden cuatro.
Si el cuadrado mágico tiene cinco filas y cinco columnas, es decir veinticinco casillas y veinticinco números, se denomina cuadrado mágico de orden cinco.
En general, si el cuadrado mágico tiene "n" filas y "n" columnas, es decir n2 casillas y n2 números, se denominará cuadrado mágico de orden "n".
No existen cuadrados mágicos de orden dos.
HISTORIA DE LOS CUADRADOS MÁGICOS
El origen de los cuadrados mágicos es muy antiguo, anterior a la era cristiana. Una leyenda china cuenta que alrededor del año 2200 a. C. el emperador Yu vio a las orillas del río Amarillo un cuadrado mágico grabado en el caparazón de una tortuga. Se denominó
«LO-SHU» y se le atribuyeron propiedades mágicas y religiosas.
En Occidente los cuadrados mágicos aparecen por primera vez en el año 130 d.C. en los trabajos del astrónomo griego Teón de Esmirna.
En la Edad Media los cuadrados mágicos se usaron en Europa para predecir el futuro, curar enfermedades y como amuletos para prevenir plagas y maleficios. Incluso en algunas cortes europeas se grabaron cuadrados mágicos en los platos para prevenir posibles envenenamientos a los comensales.
Cornelio Agrippa (1486-1535) en su obra «Filosofía oculta» los llamó «Tabula in abaco».
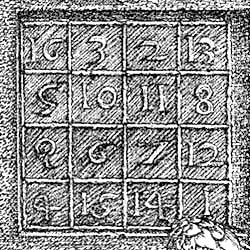
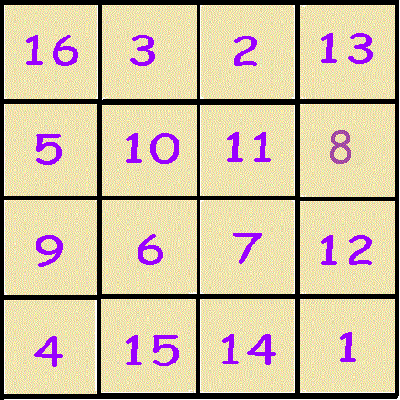
En el Renacimiento, los cuadrados mágicos se estudiaron desde el punto de vista matemático y varios científicos y artistas los usaron como ilustraciones para sus obras. Durero (1471-1528) en su grabado «Melancolía» inscribió un cuadrado mágico de orden 4, cuya constante mágica es 34. Ademas las dos cifras centrales inferiores (15 y 14) representan el año 1514 en que Durero realizó la obra.
Con el paso del tiempo científicos y matemáticos estudiaron sus propiedades matemáticas. Benjamín Franklin (1706-1790) dedicó mucho tiempo a estudiar y crear cuadrados mágicos.
En la fachada de la Pasión de la Sagrada Família de Barcelona, se encuentra un bajorrelieve de un cuadrado mágico de orden 4, obra del escultor Josep María Subirachs, que repite algunos números para conseguir que la constante mágica sea 33, la edad con la que murió Cristo.
ALGUNOS CUADRADOS MÁGICOS
Constante mágica = 15
Constante mágica = 34
ACTIVIDADES QUE PROPONEMOS PARA NIÑOS DE DIEZ O MÁS AÑOS DE EDAD
1) En un cuadrado mágico de orden tres coloca los números del 1 al 9 de forma que la constante mágica sea 15.
2) En un cuadrado mágico de orden tres coloca los números del 4 al 12 de forma que la constante mágica sea 24.
3) En un cuadrado mágico de orden cuatro coloca los números del 1 al 16 de forma que la constante mágica sea 34.
4) En un cuadrado mágico de orden cinco coloca los números del 1 al 25 de forma que la constante mágica sea 65.
5) Completa los siguientes cuadrados mágicos:
Todos los textos de «Matemáticas para niños» han sido elaborados por el equipo de «El huevo de chocolate» y pueden ser reproducidos, con fines educativos o lúdicos, con autorización previa de sus autores y citando la autoría.
| Más Matemáticas para niños | Volver a la página principal |
